Два сосуда содержат растворы кислоты различной концентрации — такие задачи ОГЭ и ЕГЭ по математике сложнее обычных задач на смеси и сплавы.
Задача
Имеется два сосуда, содержащие 48 кг и 42 кг раствора кислоты различной концентрации. Если их слить вместе, то получим раствор, содержащий 42% кислоты. Если же слить равны е массы этих растворов, то полученный раствор будет содержать 40% кислоты. Сколько килограммов кислоты содержится во втором растворе?
Решение:
Пусть концентрация первого раствора составляет x%, концентрация второго раствора — y%.
Тогда количество кислоты в первом растворе равно
![\[ \frac{x}{{100}} \cdot 48 = \frac{{x \cdot 48}}{{100}} = 0,48x \]](https://www.algebraclass.ru/wp-content/ql-cache/quicklatex.com-c26aa57a91c8e29223d13df09f024b1d_l3.png "Rendered by QuickLaTeX.com")
килограммов, во втором —
![\[ \frac{y}{{100}} \cdot 42 = \frac{{y \cdot 42}}{{100}} = 0,42y \]](https://www.algebraclass.ru/wp-content/ql-cache/quicklatex.com-23b2faf17d4d422107e6f25b937fdc79_l3.png "Rendered by QuickLaTeX.com")
килограммов.
Третий раствор получили, слив первый и второй растворы вместе. Значит масса третьего раствора равна 48+42=90 кг.
Так как концентрация третьего раствора равна 42%, то он содержит 0,42·90=37,8 кг кислоты.
Эти рассуждения удобно записывать в виде таблицы:
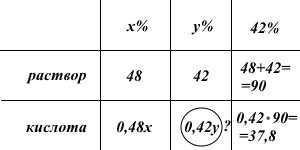
(Чтобы не ошибиться в нескольких переменных, рекомендую выделять искомую величину).
Составим первое уравнение: 0,48x+0,42y=37,8
Если слить равные массы этих растворов, то полученный раствор будет содержать 40% кислоты.
В качестве равных масс растворов можно брать любое количество — 1 кг, 100 кг или любую другую величину.
Поскольку мы ищем 0,42y, для решения системы уравнения способом сложения нужно будет «убрать» 0,48x. Поэтому в качестве равных масс удобно взять по 48 кг обоих растворов:
Составим второе уравнение: 0,48x+0,48y=38,4.
Составим систему и решим её:
![\[ \left\{ \begin{array}{l} 0,48x + 0,42y = 37,8\_\_\left| { \cdot ( - 1)} \right. \\ 0,48x + 0,48y = 38,4 \\ \end{array} \right. \]](https://www.algebraclass.ru/wp-content/ql-cache/quicklatex.com-4d867f637111488482ff944b7844846b_l3.png "Rendered by QuickLaTeX.com")
Умножим первое уравнение системы на (-1) и сложим полученное уравнение со вторым
![\[ + \frac{{\left\{ \begin{array}{l} - 0,48x - 0,42y = - 37,8 \\ 0,48x + 0,48y = 38,4 \\ \end{array} \right.}}{{0,06y = 0,6}} \]](https://www.algebraclass.ru/wp-content/ql-cache/quicklatex.com-fc8cdc11f207520df1f464467c9bd826_l3.png "Rendered by QuickLaTeX.com")
y=0,6:0,06
y=10
Количество кислоты во втором растворе равно 0,42·10=4,2 кг.
Ответ: 4,2 кг