Координатные четверти

Выясним, как в тригонометрии координатные четверти связаны с градусной и радианной мерой углов.

Тригонометрические углы получают в результате поворота луча OP₀вокруг точки O. Поэтому точка P₀ соответствует углу 0°.

При положительном направлении обхода поворот луча происходит по часовой стрелке. Градусная мера всей окружности равна 360°. Каждая из четвертей занимает угол в 90°.

Таким образом,

I координатной четверти соответствуют углы от 0° до 90°,

II — от 90° до 180°,

III — от 180° до 270°,

IV — от 270° до 360°.

Переводя градусную меру в радианную, получим аналогичное разбиение окружности по координатным четвертям в радианах:

$I:0 < \alpha < \frac{\pi }{2},$

$II:\frac{\pi }{2} < \alpha < \pi ,$

$III:\pi < \alpha < \frac{{3\pi }}{2},$

$IV:\frac{{3\pi }}{2} < \alpha < 2\pi .$

koordinatnye-chetverti

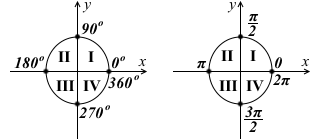
Углы 0°, 90°, 180°,270°, 360° не принадлежат ни одной из координатных четвертей.

Отрицательные значения углов получают поворотом луча против часовой стрелки. Соответственно, иллюстрация разбиения по координатным четвертям в этом случае выглядит так:

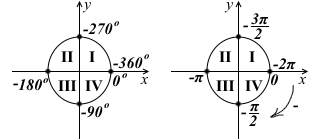
ugly-v-koordinatnyh-chetvertyah

Примеры.

Определить, углом какой четверти является угол:

а) 47°; -24°; 300°; 185°; -203°;1200°;

$b)\frac{\pi }{5};\frac{{7\pi }}{6};\frac{{13\pi }}{8}; - \frac{{9\pi }}{5};\frac{{19\pi }}{4}.$

Решение:

а) 47° — угол I координатной четверти, так как 0°<47°<90°;

-24° — угол IV координатной четверти, так как -90°<-24°<0°;

300° — угол IV координатной четверти, так как 270°<300°<360°;

185° лежит в III координатной четверти, так как 180°<185°<270°;

-203° лежит во II координатной четверти, так как

-180°<-203°<-270°;

1200°=120°+360°·3.

120° — угол II координатной четверти, поскольку 90°<120°<180°. Значит, 1200° также является углом II четверти.

b) π/5 — угол I координатной четверти, так как

$0 < \frac{\pi }{5} < \frac{\pi }{2};$

7π/6 — угол II координатной четверти, так как

$\pi < \frac{{7\pi }}{6} < \frac{{3\pi }}{2};$

Сравнение радианной меры угла с 0, π/2, π, 3π/2 и 2π иногда вызывает затруднения. В этом случае можно перевести радианную меру в градусную.

$\frac{{7\pi }}{6} = \frac{{7 \cdot 180^o }}{6} = 210^o$

Другой способ: если дробь неправильная, можно найти ближайшее к коэффициенту перед π в числителе число, которое делится нацело на знаменатель, и представить числитель как сумму (или разность) этого целого числа и остатка.

$\frac{{7\pi }}{6} = \frac{{6\pi + \pi }}{6} = \frac{{6\pi }}{6} + \frac{\pi }{6} = \pi + \frac{\pi }{6}$

Очевидно, что 7π/6>π. Поскольку π/6 — острый угол, то π/6<π/2. Следовательно, 7π/6<3π/2.

$\frac{{13\pi }}{8} = \frac{{16\pi - 3\pi }}{8} = \frac{{16\pi }}{8} - \frac{{3\pi }}{8} = 2\pi - \frac{{3\pi }}{8},$

$\frac{{3\pi }}{2} < 2\pi - \frac{{3\pi }}{8} < 2\pi ,$

откуда 13π/8 — угол IV координатной четверти.

$- \frac{{9\pi }}{5} = - \frac{{10\pi - \pi }}{5} = - (\frac{{10\pi }}{5} - \frac{\pi }{5}) =$

$= - 2\pi + \frac{\pi }{5}.$

$- 2\pi < - 2\pi + \frac{\pi }{5} < - \frac{{3\pi }}{2},$

значит — 9π/5 — угол I четверти.

$\frac{{19\pi }}{4} = \frac{{20\pi - \pi }}{4} = \frac{{20\pi }}{4} - \frac{\pi }{4} =$

$= 5\pi - \frac{\pi }{4} = 2\pi \cdot 2 + \pi - \frac{\pi }{4}.$

$\frac{\pi }{2} < \pi - \frac{\pi }{4} < \pi ,$

Следовательно, 19π/4 — угол II четверти.

Добавить комментарий Отменить ответ