Моторная лодка прошла и вернулась обратно

Задачи, в которых сказано, что моторная лодка прошла и вернулась обратно (по течению-против течения) обычно сводятся к двум случаям: сравнивается время на путь против течения и по течению либо известно общее время, затраченное на путь туда и обратно.

При этом скорость лодки по течению реки равна сумме скоростей: собственной скорости лодки и скорости течения, скорость лодки против течения равна разности этих скоростей.

За x обычно принимают неизвестную величину, которую требуется найти (собственную скорость лодки или скорость течения реки).

Если время выражено в минутах, то его следует перевести в часы:

Задача 1

Моторная лодка прошла против течения реки 208 км и вернулась в пункт отправления, затратив на обратный путь на 5 часов меньше, чем на путь против течения. Найдите скорость лодки в неподвижной воде, если скорость течения реки равна 5 км/ч.

Решение:

Пусть скорость лодки в неподвижной воде равна x км/ч.

motornaya-lodka-proshla-i-vernulas-obratno

Составим уравнение и решим его:

$\frac{{208}}{{x - 5}} - \frac{{208}}{{x + 5}} = 5$

$\frac{{208^{^{\backslash (x + 5)} } }}{{x - 5}} - \frac{{208^{^{\backslash (x - 5)} } }}{{x + 5}} = 5^{\backslash (x^2 - 25)}$

$\frac{{208(x + 5) - 208(x - 5) - 5(x^2 - 25)}}{{(x - 5)(x + 5)}} = 0$

$\frac{{ - 5x^2 + 2205}}{{(x - 5)(x + 5)}} = 0\_\_\left| {:5} \right. \Leftrightarrow \left\{ \begin{array}{l} x^2 - 441 = 0; \\ (x - 5)(x + 5) \ne 0 \\ \end{array} \right.$

x²=441; x≠±5

x₁=21 или x₂=-21 — не удовлетворяет условию задачи, так как скорость не может быть отрицательным числом.

Скорость лодки в неподвижной воде равна 21 км/ч.

Ответ: 21 км/ч.

Задача 2

Моторная лодка прошла по течению 24 км и вернулась обратно, затратив на обратный путь на 20 минут меньше, чем при движении против течения. Найдите скорость лодки в неподвижной воде, если скорость течения равна 3 км/ч.

Решение:

Пусть собственная скорость лодки в неподвижной воде (то есть собственная скорость лодки) равна x км/ч.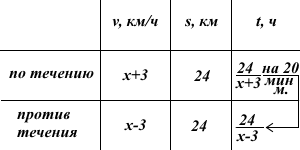 motornaya-lodka-proshla

Время переводим из минут в часы:

Составим уравнение и решим его:

$\frac{{24^{\backslash 3(x + 3)} }}{{x - 3}} - \frac{{24^{\backslash 3(x - 3)} }}{{x + 3}} = \frac{{1^{\backslash (x^2 - 9)} }}{3}$

$\frac{{72(x + 3) - 72(x - 3) - (x^2 - 9)}}{{(x - 3)(x + 3)}} = 0$

$\frac{{72x + 216 - 72x + 216 - x^2 + 9}}{{(x - 3)(x + 3)}} = 0$

$\frac{{ - x^2 + 441}}{{(x - 3)(x + 3)}} = 0\_\_\left| { \cdot ( - 1)} \right. \Leftrightarrow$

$\Leftrightarrow \left\{ \begin{array}{l} x^2 - 441 = 0; \\ x \ne 3,x \ne - 3 \\ \end{array} \right.$

x²=441

x₁=21 или x₂=-21 не удовлетворяет условию задачи.

Скорость лодки в неподвижной воде равна 21 км/ч.

Ответ: 21 км/ч.

Задача 3

Баржа прошла по течению реки 88 км и, повернув обратно, прошла ещё 72 км, затратив на весь путь 10 часов. Найдите собственную скорость баржи, если скорость течения реки равна 5 км/ч.

Решение:

Пусть x км/ч собственная скорость баржи.

barzha-proshla-po-techeniyu-reki