Смешали два раствора вещества

Смешали два раствора вещества или в раствор добавили воду — такие задачи из ОГЭ и ЕГЭ являются самыми простыми из задач на смеси и сплавы.

Задача 1

Смешали 4 литра 35-процентного раствора вещества с 11 литрами 5-процентного раствора этого же вещества. Сколько процентов составляет концентрация получившегося раствора?

Решение:

Пусть концентрация получившегося раствора составляет x %.

Так как 1-й раствор 35-процентный, то в 4 литрах этого раствора содержится 0,35·4=1,4 литра вещества.

Так как 2-й раствор 5-процентный, то в 11 литрах этого раствора содержится 0,05·11=0,55 литров вещества.

Так как новый раствор получили, смешав 4 литра и 11 литров разных растворов, то объем нового раствора равен 4+11=15 литров.

Так как 1-й раствор содержит 1,4 литра вещества, второй — 0,55 литров вещества, то новый раствор содержит 1,4+0,55=1,95 литров вещества.

Эти рассуждения удобно оформить в виде таблицы:

Концентрация вещества в растворе равна

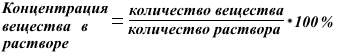
Таким образом, концентрация получившегося раствора

Ответ: 13%.

Задача 2

В сосуд, содержащий 5 литров 27-процентного водного раствора вещества, добавили 4 литра воды. Сколько процентов составляет концентрация получившегося раствора?

Решение:

Пусть концентрация получившегося раствора составляет x %.

Так как концентрация раствора составляет 27%, то 5 литров раствора содержат 0,27·5=1,35 литров вещества.

После добавления 4 литров воды количество раствора стало равным 5+4=9 литрам, количество вещества не изменилось.

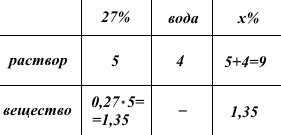
Концентрация получившегося раствора составляет

Ответ: 15%.