Из пункта А в пункт В одновременно

Задача

Из пункта А в пункт В, расстояние между которыми 40 км, одновременно выехали автомобилист и велосипедист. За час автомобилист проезжает на 65 км больше, чем велосипедист. Определите скорость велосипедиста, если известно, что он прибыл в пункт В на 2 часа 10 минут позже автомобилиста. Ответ дайте в км/ч.

Решение:

Пусть x км/ч — скорость велосипедиста. Известно, что за час автомобилист проезжает на 65 км больше, чем велосипедист. Следовательно, скорость автомобилиста равна (x+65) км/ч.

Так как велосипедист прибыл в пункт В на 2 часа 10 минут позже автомобилиста, то он затратил на весь путь времени больше на

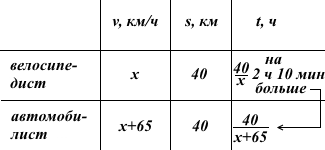
iz-punkta-a-v-punkt-v-odnovremenno

Составим уравнение и решим его:

$\frac{{40^{\backslash 6(x + 65)} }}{x} - \frac{{40^{\backslash 6x} }}{{x + 65}} = \frac{{13^{\backslash x(x + 65)} }}{6}$

$\frac{{240(x + 65) - 240x - 13x(x + 65)}}{{6x(x + 65)}} = 0$

$\frac{{ - 13x^2 - 13 \cdot 65x + 240 \cdot 65}}{{6x(x + 65)}} = 0\_\_\_\left| {:( - 13)} \right.$

$\frac{{x^2 + 65x - 1200}}{{6x(x + 65)}} = 0 \Leftrightarrow \left\{ \begin{array}{l} x^2 + 65x - 1200 = 0; \\ x \ne 0;x \ne - 65 \\ \end{array} \right.$

$x_1 = 15;x_2 = - 80$

x₂ не удовлетворяет условию задачи.
Значит, скорость велосипедиста равна 15 км/ч.

Ответ: 15 км/ч.

Добавить комментарий Отменить ответ