Функция прямая пропорциональность

Определение

Функция вида y=kx, где k — число (k≠0), называется функцией прямой пропорциональности (или функция прямая пропорциональность).

Число k называется коэффициентом пропорциональности. О переменной y говорят, что она пропорциональна переменной x.

Прямая пропорциональность — частный случай линейной функции y=kx+b (при b=0).

Графиком прямой пропорциональности является прямая, проходящая через начало координат — точку O (0;0).

Для построения графика прямой пропорциональности достаточно взять одну точку, вторая — точка O.

Свойства функции прямой пропорциональности

1) Область определения — множество действительных чисел:

D(y): x∈(-∞;+∞) (или x∈R).

2) Область значений — множество действительных чисел:

D(y): y∈(-∞;+∞) (или y∈R).

3) Нуль функции (y=0) при x=0.

4) При k>0 функция y=kx возрастает, при k<0 — убывает.

5) При k>0 график функции проходит через I и III координатные четверти.

Функция принимает положительные значения при положительных значениях аргумента:

y>0 при x>0.

Функция принимает отрицательные значения при отрицательных значениях аргумента:

y<0 при x<0.

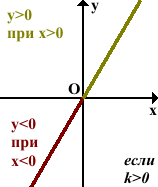
При k<0 график функции проходит через II и IV координатные четверти.

Функция принимает положительные значения при отрицательных значениях аргумента:

y>o при x<0.

Функция принимает отрицательные значения при положительных значениях аргумента:

y<0 при x>0.

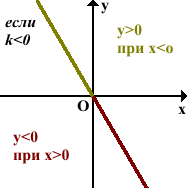
Число k называется угловым коэффициентом прямой y=kx.

k=tg α, где α — угол, который прямая образует с положительным направлением оси Ox.

Чтобы сравнить угловые коэффициенты прямых, сравниваем углы между прямыми и положительным направлением оси абсцисс.

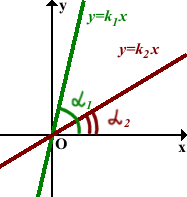
При k₁>0, k₂>0

так как α₁>α₂, то k₁>k₂.

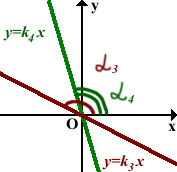
При k₃<0, k₄<0

так как α₃>α₄, то k₄>k₃.

В качестве иллюстрации рассмотрим графики четырёх функций прямой пропорциональности.

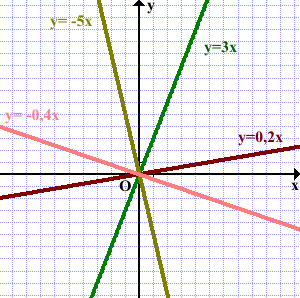
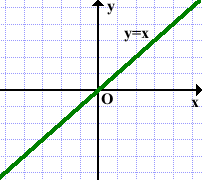
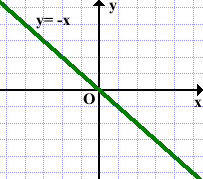
Графики функций y=x и y= -x являются биссектрисами соответственно I и III, II и IV координатных четвертей. Эти графики легко построить на листе в клеточку: каждую клеточку делим по диагонали: