Теплоход после стоянки возвращается в пункт оправления

«Теплоход после стоянки возвращается в пункт оправления» — ещё один вид задач по алгебре, которые в ОГЭ по математике включены под номером 21, а в ЕГЭ — №11.

Такие задачи можно решить, составив уравнение. За x обычно принимают либо собственную скорость теплохода (баржи), либо скорость течения (что неизвестно, то и берём за x). Если скорость известна, за x можно принять время или расстояние.

Задача 1

Теплоход проходит по течению реки 210 км и после стоянки возвращается в пункт оправления. Найдите скорость теплохода в неподвижной воде , если скорость течения реки равна 4 км/ч, стоянка длится 9 часов, а в пункт отправления теплоход возвращается через 27 часов после отплытия из него.

Решение:

Пусть скорость теплохода в неподвижной воде равна x км/ч.

Так как стоянка длится 9 часов, а в пункт отправления теплоход возвращается через 27 часов после отплытия из него, то на весь путь теплоход затратил 27-9=18 часов.

teplohod-posle-stoyanki-vozvrashchaetsya

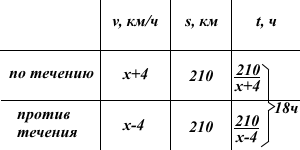
Составим уравнение и решим его:

$\frac{{210}}{{x + 4}} + \frac{{210}}{{x - 4}} = 18\_\_\left| {:6} \right.$

$\frac{{35^{\backslash (x - 4)} }}{{x + 4}} + \frac{{35^{\backslash (x + 4)} }}{{x - 4}} = 3^{\backslash (x^2 - 16)}$

$\frac{{35(x - 4) + 35(x + 4) - 3(x^2 - 16)}}{{(x - 4)(x + 4)}} = 0$

$\frac{{35x - 140 + 35x + 140 - 3x^2 + 48}}{{(x - 4)(x + 4)}} = 0$

$\frac{{ - 3x^2 + 70x + 48}}{{(x - 4)(x + 4)}} = 0\_\_\left| {:( - 1)} \right.$

$\Leftrightarrow \left\{ \begin{array}{l} 3x^2 - 70x - 48 = 0; \\ x \ne 4;x \ne - 4 \\ \end{array} \right.$

3x²-70x-48=0

$D = b^2 - 4ac = 70^2 - 4 \cdot 3 \cdot 48 = 5476,$

$x_{1,2} = \frac{{ - b \pm \sqrt D }}{{2a}} = \frac{{70 \pm 74}}{6}$

x₁=24 или x₂=-2/3 — не удовлетворяет условию задачи.

Скорость теплохода в неподвижной воде равна 24 км/ч.

Ответ: 24 км/ч.

Задача 2

Баржа в 10:00 вышла из пункта А в пункт В, расположенный в 15 км от А. Пробыв в пункте В 1 час 20 минут, баржа отправилась назад и вернулась в пункт А в 18:00. Определите (в км/ч) скорость течения реки, если известно, что собственная скорость баржи равна 6 км/ч.

Решение:

Пусть скорость течения реки равна x км/ч.

Так как баржа вышла из пункта А в 10:00, вернулась назад в 18:00, пробыла в пункте В 1 час 20 минут, то на весь путь она затратила 18 часов-10 часов -1 час 20 минут=6 часов 40 минут. Выразим время в часах:

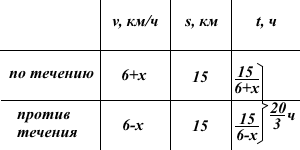
barzha-vyshla-iz-punkta-a-v-punkt-b

Составим и решим уравнение:

$\frac{{15}}{{6 + x}} + \frac{{15}}{{6 - x}} = \frac{{20}}{3}\_\_\left| {:5} \right.$

$\frac{{3^{\backslash 3(6 - x)} }}{{6 + x}} + \frac{{3^{\backslash 3(6 + x)} }}{{6 - x}} = \frac{4}{3}^{\backslash (36 - x^2 )}$

$\frac{{9(6 - x) + 9(6 + x) - 4(36 - x^2 )}}{{3(6 + x)(6 - x)}} = 0$

$\frac{{54 - 9x + 54 + 9x - 144 + 4x^2 }}{{3(6 + x)(6 - x)}} = 0$

$\frac{{4x^2 - 36}}{{3(6 + x)(6 - x)}} = 0\_\_\left| {:4 \Leftrightarrow } \right.$

$\Leftrightarrow \left\{ \begin{array}{l} x^2 - 9 = 0; \\ x \ne - 6;x \ne 6 \\ \end{array} \right.$

x²-9=0

x₁=3 или x₂=-3 — не удовлетворяет условию задачи.

Ответ: 3 км/ч.

Задача 3

Теплоход, скорость которого в неподвижной воде равна 27 км/ч, проходит некоторое расстояние по реке и после стоянки возвращается в исходный пункт. Скорость течения равна 1 км/ч, стоянка длится 5 часов, а в исходный пункт теплоход возвращается через 32 часа после отправления из него. Сколько километров проходит теплоход за весь рейс?

Решение:

Так как в исходный путь теплоход возвращается через 32 часа после отправления из него, а стоянка длится 5 часов, то общее время в пути равно 32-5=27 часов.

Скорость теплохода в неподвижной воде равна 27 км/ч, скорость течения реки равна 1 км/ч. Значит, по течению теплоход движется со скоростью 27+1=28 км/ч, против течения — 27-1=26 км/ч.

Пусть x часов — время движения теплохода по течению, тогда (27-x)ч — время движения против течения. 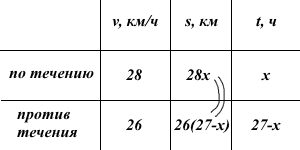teplohod-posle-stoyanki

По течению и против течения теплоход прошёл одинаковое расстояние. Составим уравнение и решим его:

28x=26(27-x)

28x=702-26x

28x+26x=702

54x=702

x=13

13 часов — время движения теплохода по течению. За это время он прошёл 28·13=364 км.

Значит, за весь рейс теплоход прошёл 364+364=728 км.

Ответ: 728 км.

Добавить комментарий Отменить ответ