Стандартный вид числа

Определение

Стандартный вид числа — это его запись в виде произведения

где

Число n называется порядком числа, записанного в стандартном виде.

В стандартном виде можно записать любое положительное число.

Как правило, стандартный вид числа используют для записи больших и малых величин.

Примеры.

Записать число в стандартном виде и указать порядок числа:

1) 8 765 000;

2) 12 346 000 000;

3) 723,4;

4) 0,00123;

5) 0,000057;

6) 0,000729;

7) 5430·10⁵;

8) 0,0321·10⁸;

Решение:

Чтобы записать число в стандартном виде, надо представить его в виде произведения, первый множитель которого — число от единицы до десяти (1≤a<10), второй — степень десяти.

1) Число 8 765 000 больше 10. Запятой в числе не видим, значит, по умолчанию она находится в конце записи:

8 765 000= 8 765 000,

Если перенести запятую влево на 6 знаков, получим число, большее 1 и меньшее 10:

На 6 знаков влево запятую переносим при делении числа на миллион:

1 000 000 =10⁶, то есть данное число разделили на 10⁶. Чтобы число не изменилось, умножаем результат на 10⁶:

Получили число, записанное в стандартном виде. Его порядок n=6.

При решении примеров на приведение числа к стандартному виду удобнее деление числа на 

заменить умножением на

то есть

Итак, для приведения к стандартному виду числа, больше либо равного 10, запятую в его  записи переносим влево на n цифр и результат умножаем на 10 в степени n:

2) 12 346 000 000=12 346 000 000,
Чтобы величина первого множителя входила в промежуток от 1 до 10, надо запятую в записи данного числа перенести на 10 знаков влево, а чтобы число не изменилось, умножить результат на 10¹º:

Это число записано в стандартном виде. Его порядок n=10.

3) 723,4

Чтобы первый множитель соответствовал условию 1≤a<10, нужно перенести запятую в записи числа на 2 цифры влево. Чтобы число не изменилось, умножим результат на 10²:

723,4=7,234·10².

Результат — число, записанное в стандартном виде. Его порядок n=2.

4) Чтобы первый множитель в стандартной записи числа удовлетворял условию  1≤a<10, запятую в 0,00123 нужно перенести на 3 цифры вправо

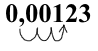
что соответствует умножению числа на 10³. Чтобы число не изменилось, результат умножаем на 10 в минус третьей степени:

Порядок числа n= -3.

Таким образом, для приведения к стандартному виду числа, меньшего единицы, запятую в его записи переносим на n цифр вправо и результат умножаем на 10 в степени -n:

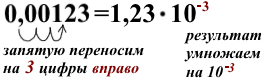
Переносим запятую в записи числа на 5 цифр вправо (что соответствует умножению числа на 10⁵). Результат умножаем на 10 в минус пятой степени. Порядок числа n= -5.

Порядок числа n= -4.

Число 5430 представляем в стандартном виде. Для этого запятую в его записи переносим на 3 цифры влево и результат умножаем на 10³.

Далее выполняем умножение степеней с одинаковыми основаниями.

Порядок числа n=6.

Порядок числа n=6.

Порядок числа n= -4.

Порядок числа n= -10.

Сравнение чисел, записанные в стандартном виде

• Сравниваем порядок чисел. Число с большим порядком больше числа с меньшим порядком.
• Если числа имеют одинаковые порядки, сравнивают первые множители произведения.

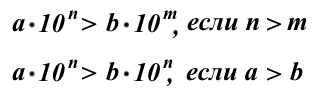
Примеры

так как порядок первого числа больше порядка второго числа (8>7);

поскольку порядок первого числа меньше порядка второго числа (-8<-7);

так как при равных порядках первый множитель у первого числа больше, чем у второго (3,4>2,97).