График функции y=f(x)/k

График функции y=f(x)/k  (где k>1) может быть получен из графика функции y=f(x) с помощью сжатия к оси Ox в k раз.

При таком преобразовании каждая точка (x; y) графика функции y=f(x) переходит в точку (x; y/k) графика функции y=f(x)/k:

(x; y) → (x; y/k)

(то есть абсцисса (x) каждой точки начального графика остаётся неизменной, а ордината (y) уменьшается в k раз).Точки, лежащие на оси Ox при сжатии к оси абсцисс остаются на месте (так как 0/k=0).

Примеры.

1) График функции y=x²/3 можно получить из графика функции y=x² сжатием к оси Ox в 3 раза.

Строим параболу y=x² (достаточно отметить базовые точки). Координату x каждой точки оставляем без изменения, координату y делим на 3.

(1; 1) → (1; 1/3),

(-1; 1) → (-1; 1/3),

(2; 4) → (2; 4/3),

(-2; 4) → (-2; 4/3),

(3; 9) → (3; 3),

(-3; 9) → (-3; 3).

Таким образом, каждая точка нового графика соответственно располагается под точкой первоначального графика, но в 3 раза ближе к оси абсцисс.

Вершина параболы при сжатии к оси Ox остаётся на месте (0:3=0).

2) График функции y=x³/4 может быть получен из графика функции y=x³ сжатием к оси абсцисс в 4 раза.

Для построения графика абсциссы базовых точек графика кубической функции оставляем неизменными, а каждую ординату делим на 4:

(1; 1) → (1; 1/4),

(-1; -1) → (-1; -1/4),

(2; 8) → (2; 8/3),

(-2; 8) → (-2; -8/3).

Точка (0; 0) при таком преобразовании остаётся на месте.

3) График функции y=(1/2)√x можно получить сжатием к оси Ox графика функции y=√x.

Координату x каждой из базовых точек графика y=√x оставляем без изменений, координату y делим на 2:

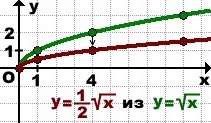
(0; 0) →  (0; 0),

(1;1) →  (1; 1/2),

(4; 2) →  (4; 1),

(9; 3) → (9; 9/2)  и т. д.

Геометрические преобразования дают возможность на основании графиков элементарных функций строить многие другие графики. Умение строить графики  функций востребовано при решений заданий из различных разделов алгебры.