График функции y=f(|x|)

График функции y=f(|x|) может быть получен из графика функции y=f(x).

Для этого ту часть графика, которая лежит левее оси Oy, отбрасываем. Часть графика, расположенную правее оси ординат, сохраняем, и её же отображаем симметрично относительно оси Oy.

Точка, лежащая на оси Oy, при таком преобразовании остаётся на месте.

Примеры.

1) Построить график функции y= -x²+2|x|+8.

Решение:

Так как x²=|x|², запишем формулу функции в виде y= —|x|²+2|x|+8.

График функции y= —|x|²+2|x|+8 можно получить из графика функции y= -x²+2x+8. Для этого часть графика, лежащую слева от оси Oy, отбрасываем. Правее оси ординат график сохраняем и это же часть отображаем симметрично относительно оси Oy:

(1; 9) → (-1; 9),

(2; 8) → (-2; 8),

(3; 5) → (-3; 5),

(4; 0) → (-4; 0).

График y= -|x|²+2|x|+8 из графика y= -x²+2x+8.

2) График функции

получен из графика функции y=-4/(x-2).

Всё, что лежит левее оси Oy, отбрасываем, всё, что правее — отображаем симметрично относительно оси ординат:

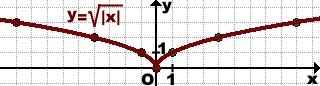
3) График функции

получен из графика y=√x.

Отбрасывать здесь нечего, поскольку график полностью расположен правее оси ординат. Весь график сохраняем, и его же отображаем симметрично относительно оси Oy:

Геометрические преобразования — быстрый и удобный способ построения графиков на основе графиков элементарных функций. Поскольку в алгебре строить графики приходится достаточно часто, важно вовремя научиться пользоваться этим инструментом.