График кусочно заданной функции

Построить график кусочно заданной функции — один из видов задания 23 из ОГЭ по математике.

Рассмотрим примеры построения таких графиков.

1) Постройте график функции

и определите, при каких значениях m прямая y=m имеет с графиком ровно две общие точки.

Решение:

Область определения функции D(y): x∈R.

График данной функции состоит из трёх частей.

Значения x=3 и x=4 разбивают числовую прямую на три промежутка, на каждом из которых рассмотрим отдельную функцию.

Соответственно, прямые  x=3 и x=4 разбивают координатную плоскость на три области.

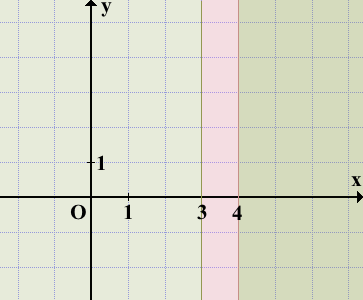
Каждый из графиков строится в своей области и не должен выходить за её пределы.

Чтобы не нарушить это правило, можно прямые x=3 и x=4 (прямые, параллельные оси Oy) выделить на черновике тонкой линией либо пунктиром. В чистовой вариант, разумеется, их переносить не нужно.

Итак, рассмотрим на трёх промежутках три различные функции.

1) Если x<4, y=2x-2.

y=2x-2 — линейная функция. Графиком линейной функции является прямая. Для построения прямой достаточно взять две точки.

При x=0 y=2·0-2=-2, получили точку (0;-2).

При x=2 y=2·2-2=2, получили точку (2;2).

Обычно для построения графика оформляют таблицу:

Значения x можно брать, вообще говоря, любые. Главное, не забыть, что данная прямая не должна выходить правее x=3. Поэтому всё же лучше выбирать x, удовлетворяющие условию x<3.

2) Если 3≤x≤4, y=-3x+13.

y=-3x+13 — линейная функция. График — прямая. Для построения прямой берём две точки.

3) Если x>4, y=1,5x-5.

y=1,5x-5 — линейная функция. График — прямая. для построения прямой берём две точки.

Отметим каждую пару точек и проведём через них прямые, не забывая об ограничениях.

Получим график, состоящий их двух лучей и одного отрезка:

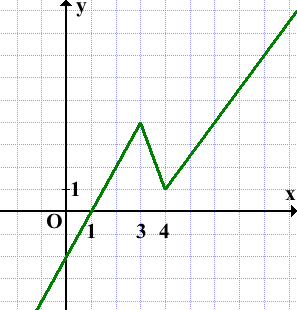
Прямая y=m имеет с графиком ровно две общие точки, если она проходит через точки соединения двух частей графика, то есть при m=1 и m=4:

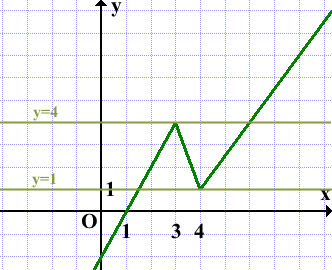
Ответ: 1; 4.

2) Постройте график функции

и определите, при каких значениях m прямая y=m имеет с графиком ровно две общие точки.

Решение:

Область определения функции D(y): x∈R.

1) Если x≥4, y=x²-10x+27.

y=x²-10x+27 — квадратичная функция. Её график — парабола, ветви которой направлены вверх (так как a=1>0).

Ищем координаты вершины параболы.

Таким образом, (5;2) — вершина параболы.

Так как a=1, от вершины строим параболу y=x².

(Другой вариант — переписать правую часть формулы в виде y=(x²-10x+25)+2=(x-5)²+2 и построить график параллельным переносом графика y=x² на 5 единиц вправо вдоль оси Ox и на 2 единицы вверх вдоль оси Oy).

2) Если x<4, y=x-1.

y=x-1 — линейная функция. График — прямая. Для построения прямой берём две точки:

Хотя на x наложено условие x<4, для построения прямой можно брать любые значение. Главное — не забыть, что правее x=4 прямая не должна выходить.

Итак, график данной функции состоит из двух частей. Прямая x=4 разделяет плоскость на две полуплоскости. Справа от неё расположена часть параболы с вершиной в точке (5;2), слева — прямая:

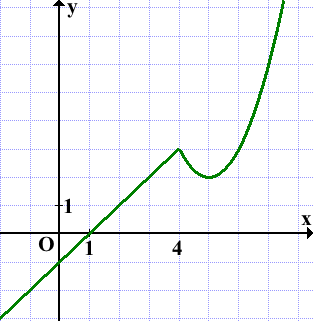
Прямая y=m имеет с графиком ровно две общие точки, если она проходит через вершину параболы и через точку соединения параболы и прямой, то есть при m=2 и m=3:

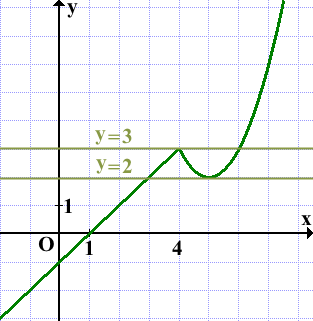
Ответ: 2; 3.

3) Построить график функции

и определить, при каких значениях m прямая y=m имеет с графиком одну или две общие точки.

Решение:

Область определения функции D(y): x∈R.

1) Если x≥-3, y=x²+4x+4.

y=x²+4x+4 — квадратичная функция. График — парабола ветвями вверх. Можно найти координаты вершины параболы и от вершины построить график функции y=x².

(Если заметить в правой части формулу квадрата суммы и переписать формулу функции y=(x+4)², то можно построить параболу параллельным переносом параболы y=x² на 4 единицы влево вдоль оси Ox).

2) Если x<-3,

— функция обратной пропорциональности. График — гипербола. Для построения гиперболы нужно взять несколько точек:

Таким образом, график данной функции состоит из двух частей. Справа от прямой x=-3 строим параболу с вершиной в точке (-2;0), слева — ветвь гиперболы:

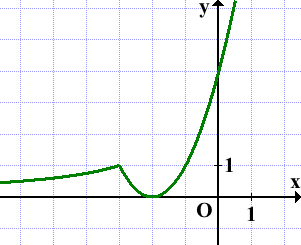
Прямая y=m имеет с графиком одну или две общие точки при m=0 и m≥1:

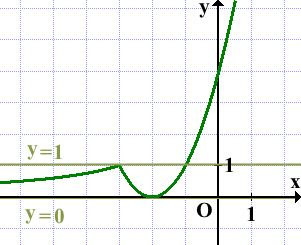
Ответ: m=0 и m∈[1;∞).